前缀树

需求

• 高效存储和检索字符串数据集中的键

• 前缀搜索和拼写检查

数组实现

插入Insert: O(1)->O(N)

搜索Search:O(N)

前缀搜索 startWith:O(NM)

Trie

Tire，又称前缀树或字典树，是一颗有根树，每个结点包含以下字段。

• 指向子节点的指针数组children,对于26字母而言，数组长度为26。此时children[0]对应a，children[1]对应b，……，children[25]对应z。

• 布尔字段isEnd,表示该结点是否为字符串的结尾

数据结构图

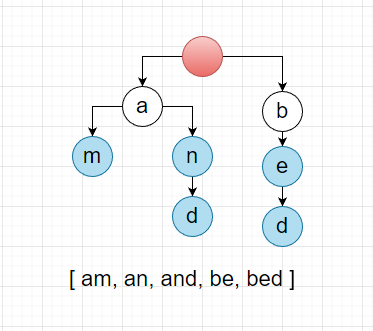
性能分析

k为字符串长度

插入Insert: O(k)

搜索Search:O(k)

前缀搜索 startWith:O(k)

数据结构实现

1. 插入字符串

   我们从字典树的根开始，插入字符串。对于当前字符对应的子节点，有两种情况：

   • 子节点存在。沿着指针移动到子节点，继续处理下一个字符。

   • 子节点不存在。创建一个新的子节点，记录在 children 数组的对应位置上，然后沿着指针移动到子节点，继续搜索下一个字符

   重复以上步骤，直到处理字符串的最后一个字符，然后将当前节点标记为字符串的结尾。

2. 查找前缀/字符串

   我们从字典树的根开始，查找前缀。对于当前字符对应的子节点，有两种情况：

   • 子节点存在。沿着指针移动到子节点，继续搜索下一个字符。

   • 子节点不存在。说明字典树中不包含该前缀，返回空指针。

   重复以上步骤，直到返回空指针或搜索完前缀的最后一个字符。若搜索到了前缀的末尾，就说明字典树中存在该前缀。此外，若前缀末尾对应节点的 isEnd为真，则说明字典树中存在该字符串。

class TrieNode {
public:
    vector<TrieNode*> children;
    bool isWord;
    TrieNode() : isWord(false), children(26, nullptr) {
    }
    ~TrieNode() {
        for (auto& c : children)
            delete c;
    }
};

class Trie {
public:
    /** Initialize your data structure here. */
    Trie() {
        root = new TrieNode();
    }
    
    /** Inserts a word into the trie. */
    void insert(string word) {
        TrieNode* p = root;
        for (char a : word) {
            int i = a - 'a';
            if (!p->children[i])
                p->children[i] = new TrieNode();
            p = p->children[i];
        }
        p->isWord = true;
    }
    
    /** Returns if the word is in the trie. */
    bool search(string word) {
        TrieNode* p = root;
        for (char a : word) {
            int i = a - 'a';
            if (!p->children[i])
                return false;
            p = p->children[i];
        }
        return p->isWord;
    }
    
    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
        TrieNode* p = root;
        for (char a : prefix) {
            int i = a - 'a';
            if (!p->children[i])
                return false;
            p = p->children[i];
        }
        return true;
    }
private:
    TrieNode* root;
};

力扣题

• 208 实现Trie

• 720 词典中最长的单词

• 692 前k个高频单词